騒音のレベルを減衰させるために、最もシンプルな方法は音源と受音点の距離を離すことです。
図-1は音源の種類ごとの距離による幾何的な減衰量を示したものになります。

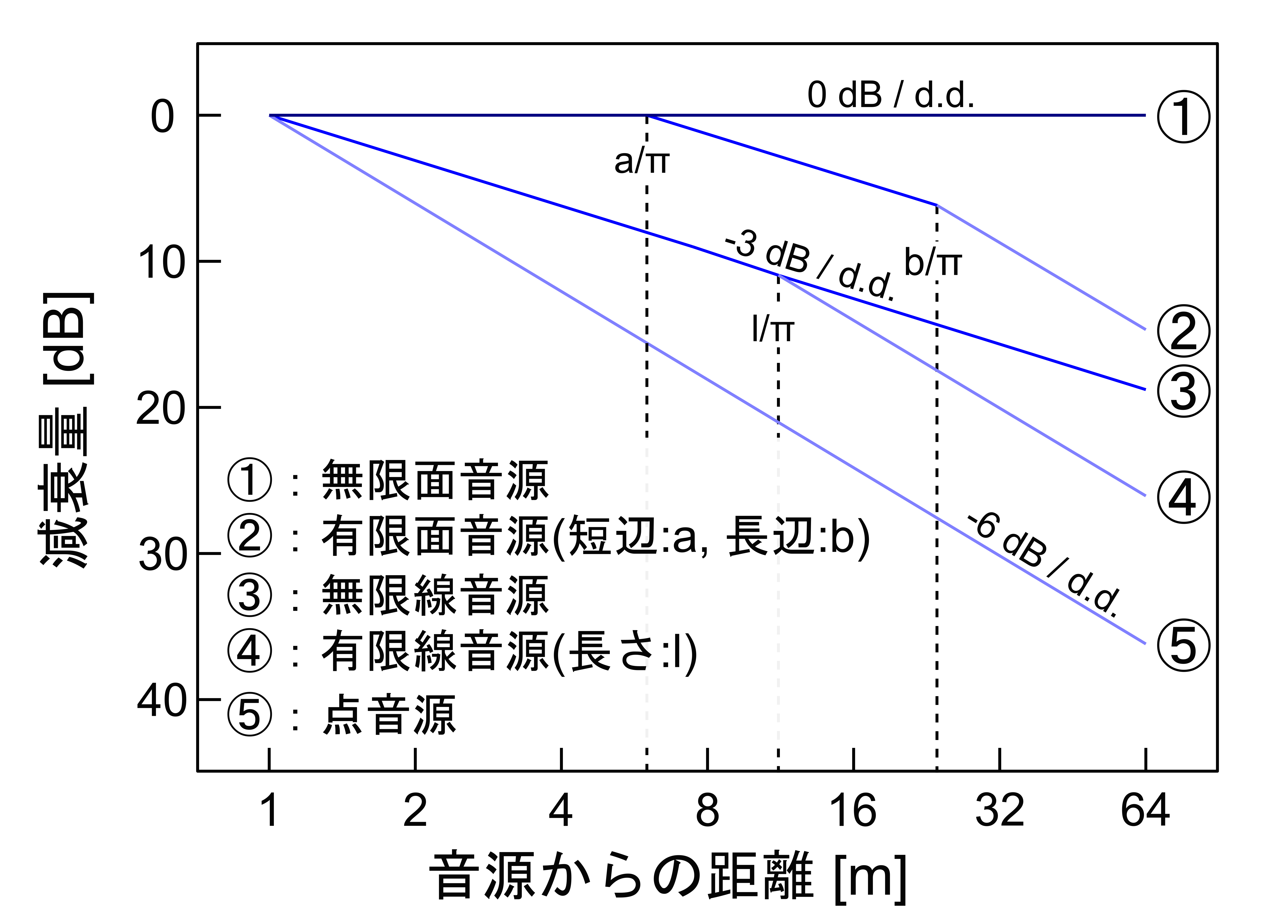図-1　音源の種類ごとの距離による減衰量

この距離減衰の計算式は、音源の種類ごとに以下のようになります。

1. 点音源からの距離減衰

自由空間にある音響パワー$W$のパワーレベルを$L_W$、点音源から距離$d$離れた点における音圧レベルを$L$とすると、

\[ L=L_W-11-20 \log d \tag{1} \]

と表すことができる。
また、半自由空間では

\[ L=L_W-8-20 \log d \tag{2} \]

となる。
ここで、点音源から$d1$、$d2$（m）離れた2地点の音圧レベルは、

\[ L_2-L_1=-20 \log \frac{d_2}{d_1} \tag{3} \]

\[ L_2=L_1-20 \log \frac{d_2}{d_1} \tag{4} \]

となり、距離$d$が2倍になるごとに6dB減衰することがわかります。

2. 線音源からの距離減衰

無限に長い線状の音源の場合には、

\[ L=L_W-8-10 \log d \tag{5} \]

となり、距離が2倍になるごとに3dBの減衰をします。

有限の長さの線音源の場合には、その長さを$l$すると、
$\frac{l}{\pi}$までは、距離が倍になるごとに3dB減衰し、それ以降は点音源と同様に倍距離で6倍減衰するようになります。

3. 面音源からの距離減衰

音源が十分に広い面的な音源の場合、音源の正面において、距離減衰は起きません。

有限の面音源の場合、短辺を$a$（m）、長辺を$b$（m）とすると、

距離が$\frac{a}{\pi}$（m）までは、距離減衰無し、
距離が$\frac{b}{\pi}$（m）までは、線音源的な減衰特性、
距離が$\frac{b}{\pi}$（m）以降は、点音源的な減衰特性となります。

指向係数Q

点音源が反射面などの影響を受けない音場（自由音場）にある場合、指向係数Q=1となります。

点音源が、大きな反射面に近傍に置かれている際には、
指向係数は、以下の簡易的な方法で設定されることがあります。

1. 1つの反射近傍に存在：$Q=2$
2. 2つの反射面が直交する交点近くに存在：$Q=4$
3. 3つの反射面が直交する隅角近くに存在：$Q=8$

これらをまとめたものを図-2に示します。

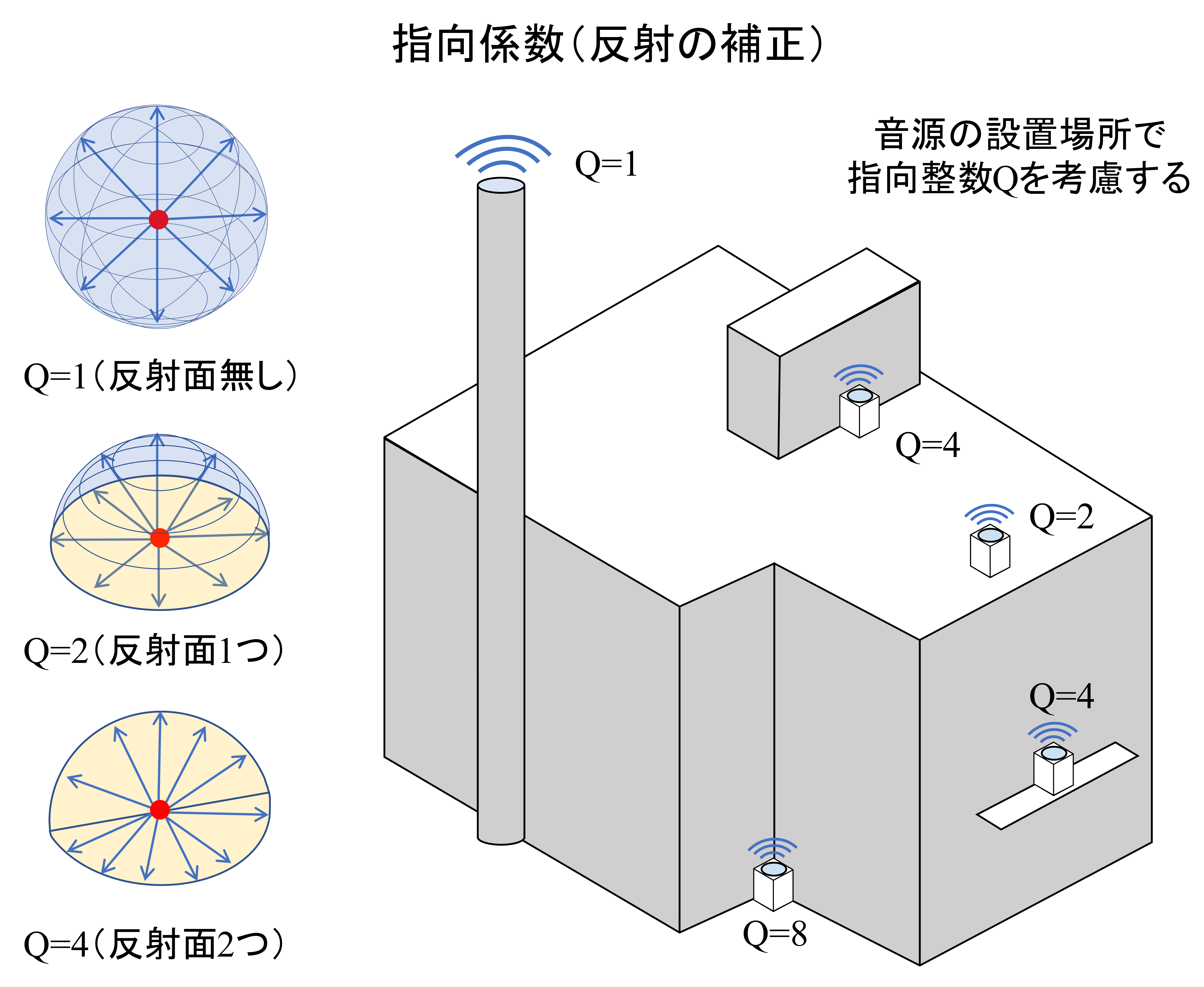
図-2　音源と反射面の位置関係による指向係数$Q$

屋外を伝搬する音は、音源からの距離が数十メートル以上になると、空気吸収、地表面や障害物、その他の気象などの影響を受け、幾何的広がりを計算した減衰より大きな減衰をします。

1. 空気の吸収による過剰減衰

湿度と温度、気圧によって変化し、周波数が低いほど、減衰は小さくなります。

2. 地表面の影響による過剰減衰

地表面で音が反射することで、音が減衰します。
この地表面による減衰は、直接伝搬する音と地面で反射して到来する音が重なりあい、互いに干渉することによって生じるため、その量は周波数、伝搬距離、音源と観測点の位置関係によって変化します。
また、平坦でない地面では、凹凸による音の錯乱によっても減衰が生じます。

3. 気象条件による過剰減衰

屋外における騒音の伝搬は気象条件によっても変化します。
雨や雪の影響は小さいですが、気温や風の分布の影響は大きいです。

昼と夜で気温の大気中における上限分布が変化することによる音の屈折も発生します。
昼は地表面付近で温度が高くなり、音は上空に曲がります。
反対に、夜は上空の方が気温が高くなり、音は地表面に曲がります。
これによって、昼間は音源から離れると音が上空に逃げ、夜は遠くまで音が届くようになります。

また、風によっても音は屈折します。
上空になるほど風速が上がるので、風上に向かっては音は上空に逃げ、風下に向かっては遠方まで音が良く届くようになります。

参考文献：前川 純一他. 建築・環境音響学 第3版. 共立出版. 2011